Táto práca vyhodnocuje možnosti aplikácie diferenciálnej a lineárnej kryptoanalýzy odvodeného redukovaného variantu blokovej šifry na úrovni štyroch iteráciách. S ohľadom na zistené obmedzenia vytvára návrh a implementuje program, pomocou ktorého vyhodnocuje odolnosť jednotlivých redukovaných komponentov. Na základe výsledkov rekonštruuje aktívne bity kľúča poslednej iterácie a analyzuje spôsoby zefektívnenia algoritmu daného útoku. Pomocou vybraných kritérií prezentuje dosiahnuté výsledky a odhadne možnosti respektíve komplexnosť analýzy úplného variantu redukovanej šifry.
Úvod
Diferenciálna [2] a lineárna [3] kryptoanalýza existuje už niekoľko rokov a dnes tieto základné typy analýz môžeme považovať za nutnú požiadavku z hľadiska odolnosti blokových šifier so substitučno-permutačnou štruktúrou. Princíp analýz potrebujeme zohľadniť už pri návrhu jednotlivých komponentov, ktoré v blokových šifrách zabezpečujú substitúciu a permutáciu. To zvyčajne predstavuje komplexný proces implementácie špecifických výpočtov na úrovni operácii analyzovanej šifry, bez možnosti ďalšieho použitia. Problém pri testovaní predstavuje aj samotná veľkosť jednotlivých komponentov v iterácii, ktorá zvyšuje zložitosť matematických výpočtov. Riešením je analýza šifier v redukovanom tvare bez zmeny štruktúr jednotlivých operácii, ktoré zabezpečujú substitúciu a permutáciu. Výsledky dosiahnuté na úrovni takto redukovaných šifier sú transparentné a môžeme ich zovšeobecniť voči úplným variantom analyzovaných šifier. Cieľom práce je charakterizovať možnosti a obmedzenia aplikácie diferenciálnej a lineárnej analýzy odvodeného redukovaného variantu zvolenej blokovej šifry na úrovni štyroch iteráciách. Navrhnúť a implementovať program, ktorý poskytne pomocou používateľského rozhrania prostredie pre efektívnu analýzu odolnosti jednotlivých komponentov redukovaných variantov blokových šifier voči avizovaným základným typom útokov. Zároveň, ak jednotlivé vrstvy šifry preukážu diferenciálne alebo lineárne závislosti s dostatočne veľkou pravdepodobnosťou, prostredie umožní rekonštruovať vybrané bity kľúča použitého v poslednej iterácii šifry.
Logická štruktúra a implementácia operácii
Najvhodnejším príkladom blokovej šifry so substitučno-permutačnou štruktúrou je vzhľadom na aktuálnosť AES. Hlavným kritériom pri návrhu štruktúry komponentov tejto šifry bola dostatočná celková komplexnosť difúzie/konfúzie a odolnosť voči diferenciálnej a lineárnej analýze. Vďaka zdokumentovanej štruktúre úplného variantu AES a podrobnej definície jej parametrov pri návrhu môžeme konštruovať redukované verzie [1] s analogickou štruktúrou a princípom fungovania. V takto redukovanej definícii predpokladáme zníženú odolnosť komponentov a tým získame akceptovateľnú výpočtovú zložitosť, ktorá umožní praktickú analýzu v krátkom čase. Redukovaný tvar jednotlivých operácii algoritmu AES, logickú štruktúru pri implementácii a ich reprezentáciu v používateľskom rozhraní definujeme v nasledujúcich bodoch.
1. Generovanie kľúčov
Kľúče sú v šifre definované v tvare poľa o veľkosti 2x2, kde každý stĺpec predstavuje jedno slovo wi o veľkosti 8 bitov. Jednotlivé slová kľúčov v iteráciách sú odvodené pomocou algoritmu zobrazeného na obrázku 1 z hlavného kľúča, ktorý je zadaný používateľom a zároveň použitý v prvej iterácii šifry. Vzhľadom na statickú 16 bitovú veľkosť môže každé slovo kľúča nadobudnúť hodnotu z uzavretého intervalu ![]() . Z toho vyplýva, že k inicializácii hlavného kľúča potrebujeme dve celé čísla z rozsahu hodnôt
. Z toho vyplýva, že k inicializácii hlavného kľúča potrebujeme dve celé čísla z rozsahu hodnôt ![]() zadané používateľom. Vstupné čísla prevedieme do binárneho tvaru a každé 4 bity s danou hodnotou predstavujú jednu časť slova wi. Tým získame kompletný hlavný kľúč reprezentovaný dvojrozmerným poľom
zadané používateľom. Vstupné čísla prevedieme do binárneho tvaru a každé 4 bity s danou hodnotou predstavujú jednu časť slova wi. Tým získame kompletný hlavný kľúč reprezentovaný dvojrozmerným poľom ![]() bez nutnosti komplexných zápisov v bitových štruktúrach. Algoritmus vygeneruje 5 kľúčov, pretože staticky definovaný počet iterácii v šifre má hodnotu 4.
bez nutnosti komplexných zápisov v bitových štruktúrach. Algoritmus vygeneruje 5 kľúčov, pretože staticky definovaný počet iterácii v šifre má hodnotu 4.
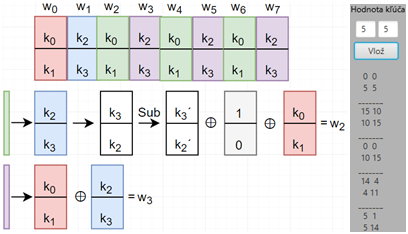
2. Substitúcia bitov Táto operácia predstavuje nelineárnu transformáciu v šifre, ktorá zabezpečuje konfúziu bitov a jej funkcionalita je zabezpečená pomocou substitučnej tabuľky vyjadrenej redukovaným predpisom. Pretože, substitúcia predstavuje jedinú nelineárnu operáciu v šifre, od jej návrhu závisí vo významnej miere odolnosť voči diferenciálnej a lineárnej kryptoanalýze. Problémom je, že väčšina šifier disponuje statickými tabuľkami, ktoré sú verejné. Takéto tabuľky majú predvídateľné statické správanie s konštantnými hodnotami a sú relatívne zraniteľné. Preto vyžadujú testovanie z pohľadu lineárnych závislostí a nerovnomerného rozdelenia bitov. Alternatívu predstavujú dynamicky definované substitučné tabuľky pomocou pseudonáhodného algoritmu. Teóriou je, že tabuľky definované náhodným generovaním hodnôt disponujú rovnakou alebo lepšou odolnosťou a vďaka inicializácii až pri samotnom šifrovaní nevyžadujú testovanie. Z tohto dôvodu v používateľskom rozhraní zobrazenom na obrázku 2 špecifikujeme viaceré možnosti generovania tabuliek, kde za predvolenú považujeme tabuľku vyjadrenú predpisom a experimentálnym porovnaním overíme teóriu odolnosti.

3. Výmena riadkov
Operácia vykoná posun prvkov druhého riadku v poli stav, kde sa nachádza reprezentácia aktuálnych medzivýsledkov jednotlivých operácii počas šifrovania. Operáciu môžeme jednoducho znázorniť v tvare
![]()
4. Kombinácia stĺpcov
Operáciu reprezentujeme ako lineárnu transformáciu jednotlivých slov poľa stav. Pretože operácia pracuje nezávisle s každým slovom, môžeme ju vyjadriť ako samostatný výpočet, ktorý spracuje jedno slovo súčasne. To využijeme pri implementácii a operáciu špecifikujeme v nasledujúcom tvare.
 Výsledkom operácie AND medzi hodnotou diferencie a konštantnou maticou sú aktívne bity v jednotlivých riadkoch Δxi. Inak povedané konštantnú matica môžeme považovať za masku, ktorá určí pozície aktívnych bitov a s ktorou sa vykoná iteratívne operácia AND. Medzi aktívnymi bitmi v každom riadku sa následne vykoná operácia XOR a výsledkom je 8 bitová matica, ktorá obsahuje 4 bitové hodnoty daných stĺpcov v poli stav.
Spolu s operáciu výmeny riadkov predstavujú v šifre komponent, ktorý zabezpečuje difúziu. Veľkosť difúzie môžeme vyhodnotiť ako základne kritérium permutačných vlastností šifry. Ak počet aktívnych substitučných tabuliek na výstupe po šifrovaní nepredstavuje minimálne dvojnásobnú hodnotu počtu aktívnych bitov na vstupe môžeme konštatovať, že šifra má slabé difúzne vlastnosti. Tento vzťah musí platiť aj keď je na vstupe aktívny len jeden bit respektíve jedna substitučná tabuľka.
Výsledkom operácie AND medzi hodnotou diferencie a konštantnou maticou sú aktívne bity v jednotlivých riadkoch Δxi. Inak povedané konštantnú matica môžeme považovať za masku, ktorá určí pozície aktívnych bitov a s ktorou sa vykoná iteratívne operácia AND. Medzi aktívnymi bitmi v každom riadku sa následne vykoná operácia XOR a výsledkom je 8 bitová matica, ktorá obsahuje 4 bitové hodnoty daných stĺpcov v poli stav.
Spolu s operáciu výmeny riadkov predstavujú v šifre komponent, ktorý zabezpečuje difúziu. Veľkosť difúzie môžeme vyhodnotiť ako základne kritérium permutačných vlastností šifry. Ak počet aktívnych substitučných tabuliek na výstupe po šifrovaní nepredstavuje minimálne dvojnásobnú hodnotu počtu aktívnych bitov na vstupe môžeme konštatovať, že šifra má slabé difúzne vlastnosti. Tento vzťah musí platiť aj keď je na vstupe aktívny len jeden bit respektíve jedna substitučná tabuľka.
5. Pridanie Kľúča Operácia vykoná XOR medzi prvkami poľa Stav s jednotlivými bitmi 16 bitového kľúča danej iterácie, ktorý bol odvodený z hlavného kľúča.
![]() Pre takto definovanú redukovanú blokovú šifru potrebujeme charakterizovať možnosti a obmedzenia aplikácie avizovaných útokov. Preto analyzujeme vplyv jednotlivých operácií vyjadreného redukovaného variantu AES na diferencie a lineárne aproximácie a v prípade, ak je v šifre možné vyjadriť diferenciálnu a lineárnu charakteristiku po poslednú iteráciu, rekonštruujeme vybrané aktívne bity kľúča poslednej iterácie.
Pre takto definovanú redukovanú blokovú šifru potrebujeme charakterizovať možnosti a obmedzenia aplikácie avizovaných útokov. Preto analyzujeme vplyv jednotlivých operácií vyjadreného redukovaného variantu AES na diferencie a lineárne aproximácie a v prípade, ak je v šifre možné vyjadriť diferenciálnu a lineárnu charakteristiku po poslednú iteráciu, rekonštruujeme vybrané aktívne bity kľúča poslednej iterácie.
Odolnosť a vplyv jednotlivých komponentov voči diferenciálnej a lineárnej analýze môžeme zovšeobecniť do 2 základných bodov:
1. Vytvorenie diferenciálnej a lineárnej aproximačnej tabuľky (substitučná vrstva)
Diferenciálna tabuľka identifikuje nerovnomerné rozdelenie vstupných diferencií ΔX a pre existujúce diferencie špecifikuje pravdepodobnosť ich zobrazenia ΔY na výstupe danej substitučnej tabuľky. Maximálnu hodnotu zobrazenia diferenciálu (ΔX, ΔY) môžeme považovať za mieru kvality návrhu respektíve odolnosti analyzovanej substitučnej tabuľky.
Lineárna aproximačná tabuľka identifikuje lineárne aproximácie, ktoré predstavujú pozície aktívnych vstupných bitov s najväčšou možnou odchýlkou lineárnej pravdepodobnosti. Maximálna hodnota odchýlky vyjadruje veľkosť rozdielu od náhodného správania substitučnej tabuľky.
Jednotlivé riadky v tabuľkách na obrázku 3 predstavujú hodnoty všetkých možných vstupných bitov a stĺpce odpovedajúce výstupné hodnoty pre substitučnú tabuľku AES vyjadrenú redukovaným predpisom.
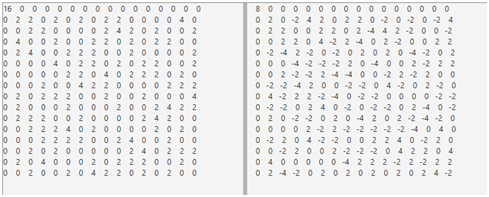
2. Konštruovanie diferenciálnej a lineárnej charakteristiky na úrovni iterácií (permutačná vrstva)
Diferenciálna analýza využíva na úrovni vstupných diferencií základnú vlastnosť operácie XOR, pomocou ktorej je definovaná operácia pridania kľúča v šifre. Ak je diferencia vyjadrená ako dve rôzne vstupné texty, zašifrované rovnakým kľúčom ∆X=(X′⊕K) ⊕ (X″⊕K) hodnota XOR medzi identickými kľúčmi K⊕K=0. Z tohto dôvodu pri tvorbe diferenciálnych charakteristík nemá pridanie kľúča žiadny vplyv.
Pretože jednotlivé diferencie vyjadrujú hodnotu bitov môžeme konštatovať, že operácie výmeny riadkov a kombinácie stĺpcov sú voči nim lineárne respektíve ich správanie identické ako pri šifrovaní vstupného textu. Inak povedané, neznemožňujú konštruovanie diferenciálnych charakteristík.
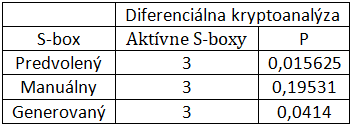
Vzhľadom nato, že každá aktívna substitučná tabuľka vo vytvorenej diferenciálnej charakteristike znižuje celkovú pravdepodobnosť zobrazenia hodnôt, stanovili sme podmienky, ktoré obmedzujú maximálny počet aktívnych substitučných tabuliek v danej iterácii na menší ako 2. Výnimkou je prvá iterácia v ktorej, kvôli univerzálnemu testovaniu uvažujeme všetky možné hodnoty vstupných diferencií a preto počet aktívnych substitučných tabuliek neobmedzujeme. Na obrázku 4 je znázornená ukážka konštrukcie aproximácie, ktorá spĺňa stanovené podmienky spolu s jej reprezentáciou v programe.
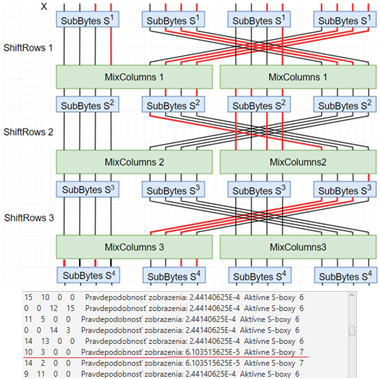
![]() , bity
, bity ![]() , ktoré vstupujú do poslednej tretej iterácie a všetky bity kľúčov, ktoré boli použité pri tvorbe aproximácie na úrovni šifry. Môžeme ju vyjadriť v tvare
, ktoré vstupujú do poslednej tretej iterácie a všetky bity kľúčov, ktoré boli použité pri tvorbe aproximácie na úrovni šifry. Môžeme ju vyjadriť v tvare
![]() Hodnota ∑K, ktorá vyjadruje operáciu XOR medzi jednotlivými bitmi kľúča nadobúda hodnotu z množiny {0,1}. Táto hodnota však pri tvorbe charakteristík ovplyvní len tvar odchýlky lineárnej pravdepodobnosti (kladný, záporný). Keďže obidve tvary považujeme za ekvivalentné, nemá pridanie kľúča na tvorbu lineárnych aproximácii žiadny vplyv.
Operácia výmeny riadkov je voči výrazu, ktorý predstavuje masku respektíve pozície aktívnych vstupných bitov lineárna. Problémom je kombinácia stĺpcov, ktorá je síce lineárna ale z definície samotnej operácie je jasná závislosť hodnoty výstupných bitov na hodnote vstupných bitov. Pretože nepracujeme s hodnotami jednotlivých bitov ale len s lineárnym výrazom nedokážeme tieto vstupné bity vyjadriť. Jediným riešením bez zásahu do štruktúry operácie je využiť všeobecný tvar zápisu operácie, ktorý hovorí, že ľubovoľný vstupný bit môžeme vyjadriť operáciou XOR ako výraz konkrétnych bitov výstupu. Tento prístup, zobrazený na obrázku 5 však vyžaduje pre vyjadrenie výstupného bitu kombinácie z aktívnych bitov na úrovni jedného slova poľa stav.
Hodnota ∑K, ktorá vyjadruje operáciu XOR medzi jednotlivými bitmi kľúča nadobúda hodnotu z množiny {0,1}. Táto hodnota však pri tvorbe charakteristík ovplyvní len tvar odchýlky lineárnej pravdepodobnosti (kladný, záporný). Keďže obidve tvary považujeme za ekvivalentné, nemá pridanie kľúča na tvorbu lineárnych aproximácii žiadny vplyv.
Operácia výmeny riadkov je voči výrazu, ktorý predstavuje masku respektíve pozície aktívnych vstupných bitov lineárna. Problémom je kombinácia stĺpcov, ktorá je síce lineárna ale z definície samotnej operácie je jasná závislosť hodnoty výstupných bitov na hodnote vstupných bitov. Pretože nepracujeme s hodnotami jednotlivých bitov ale len s lineárnym výrazom nedokážeme tieto vstupné bity vyjadriť. Jediným riešením bez zásahu do štruktúry operácie je využiť všeobecný tvar zápisu operácie, ktorý hovorí, že ľubovoľný vstupný bit môžeme vyjadriť operáciou XOR ako výraz konkrétnych bitov výstupu. Tento prístup, zobrazený na obrázku 5 však vyžaduje pre vyjadrenie výstupného bitu kombinácie z aktívnych bitov na úrovni jedného slova poľa stav.
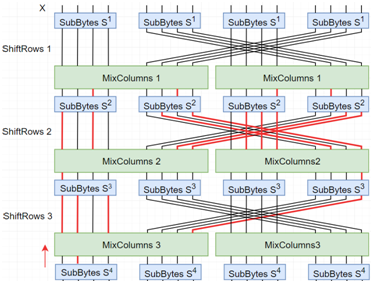
Vstupné dáta a postup testovania
Program je implementovaný objektovým návrhom v jazyku Java tak, aby poskytol jednoduché a zároveň efektívne prostredie na analýzu respektíve testovanie odolnosti komponentov blokových šifier a zároveň zabezpečil jednoduché možnosti rozšírenia analyzovaných šifrovacích algoritmov. S cieľom dosiahnuť automatizovaný a komplexný proces analýzy je vstupný text simulovaný, automatickým generovaním všetkých možných kombinácii bitov, ktoré predstavujú otvorený text v rozsahu 16 bitového bloku šifry. To znamená, že simulujeme hodnoty s ohľadom na 8 bitovú reprezentáciu jednotlivých znakov v ASCII tabuľke. Ak uvažujeme kompletnú rozšírenú tabuľku znakov ASCII, dostávame interval hodnôt ![]() z ktorého môžu obidve znaky v bloku nadobudnúť 65536 možných kombinácii bitov. Analogickým spôsobom v závislosti na pozícii aktívnych bitov je automaticky generovaná množina všetkých kombinácii kľúčov, ktoré použijeme na čiastočné dešifrovanie poslednej iterácie.
Počas testovania sme vyhodnotili lineárnu závislosť a nerovnomernosť diferenciálneho zobrazenia statických a dynamických substitučných tabuliek. Pretože sa preukázalo, že operácie testovanej redukovanej šifry, ktoré zabezpečujú permutačnú vrstvu ovplyvňujú lineárne závislosti do vysokej miery, aplikujeme na danú šifru len diferenciálnu kryptoanalýzu.
z ktorého môžu obidve znaky v bloku nadobudnúť 65536 možných kombinácii bitov. Analogickým spôsobom v závislosti na pozícii aktívnych bitov je automaticky generovaná množina všetkých kombinácii kľúčov, ktoré použijeme na čiastočné dešifrovanie poslednej iterácie.
Počas testovania sme vyhodnotili lineárnu závislosť a nerovnomernosť diferenciálneho zobrazenia statických a dynamických substitučných tabuliek. Pretože sa preukázalo, že operácie testovanej redukovanej šifry, ktoré zabezpečujú permutačnú vrstvu ovplyvňujú lineárne závislosti do vysokej miery, aplikujeme na danú šifru len diferenciálnu kryptoanalýzu.
Dosiahnuté výsledky
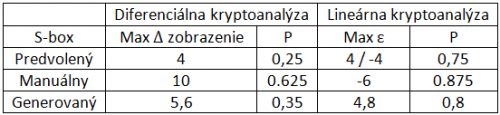
Podľa predpokladov by mala dosiahnuť najlepšie vlastnosti odolnosti substitučná tabuľka, ktorá je vyjadrená na základe predpisu. Maximálnu hodnotu zobrazenia diferencie a maximálnu odchýlku lineárnej pravdepodobnosti, ktorú počas testovania tabuľky nadobudnú, môžeme považovať za mieru kvality návrhu. Kvôli korektnosti hodnôt kritérií pre zadané a generované tabuľky vypočítame ako priemer z piatich nezávislých meraní. Ak neberieme do úvahy, že hodnoty výsledkov sú do určitej miery obmedzené veľkosťou samotnej tabuľky, môžeme konštatovať na základe výsledkov v tabuľke 1, že generované pseudonáhodné tabuľky dosahujú vo väčšine prípadov ekvivalentné vlastnosti ako tabuľka vypočítaná pri návrhu. Pre manuálne zadávané tabuľky sa zdôraznila dôležitosť korektnosti pri výpočte substitučnej vrstvy. Takto špecifikované tabuľky preukázali veľké slabiny pri rozložení jednotlivých prvkov a zároveň veľké lineárne závislosti. Na základe toho ich môžeme považovať z hľadiska bezpečnosti za nepoužiteľné.
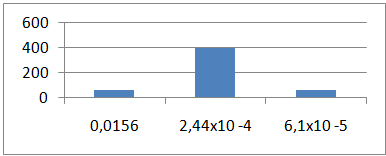


Z celkového počtu vstupných diferencií použitých pri útoku, môžeme vyjadriť efektivitu algoritmov. Základným kritériom je hodnota vyjadrená vzťahom 1/0,0156. Predpokladáme že každých 64 diferencií sa po čiastočnom dešifrovaní zobrazí minimálne jedna na hľadanú diferenciálnu charakteristiku. V prvom prípade by mala hodnota diferencie po čiastočnom dešifrovaní nadobudnúť hodnotu charakteristiky 262144 krát. To znamená, že bolo potrebných 88% z maximálneho počtu možných správnych zobrazení. Zatiaľ čo v druhom prípade z očakávaných maximálne 1024 správnych zobrazení bolo potrebných k identifikácii kľúča len 26% správnych zobrazení z maximálneho možného počtu. Môžeme teda konštatovať, že takto špecifikovaný algoritmus je efektívnejší a dosahuje transparentné výsledky.
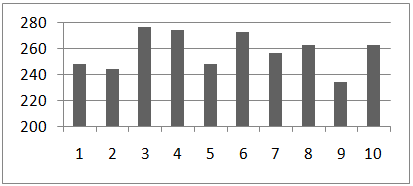
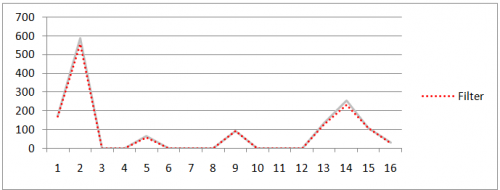
Keďže diferenciálna kryptoanalýza predstavuje útok s možnosťou výberu otvoreného respektíve šifrovaného textu, špecifikujeme dodatočnú podmienku a overíme tak ďalšiu možnosť zefektívnenia analýzy. Využijeme fakt, že zadaná diferenciálna charakteristika špecifikuje v každom prípade len dva aktívne bity, ktoré sú vstupom do poslednej iterácie. Preto môžeme s ohľadom na operácie poslednej iterácie vylúčiť zvyšné dva neaktívne bity v zašifrovanom texte. Pole kandidátnych kľúčov zobrazené na obrázku 8, definuje rozdiel výberu zašifrovaného textu na počte hodnôt, ktoré priradil algoritmus daným kľúčom.
Vyhodnotenie možností analýzy úplného variantu AES
Pri lineárnej analýze sa obmedzenie preukázalo už pri charakterizovaní vplyvu jednotlivých operácii na dané lineárne výrazy. Ako bolo zistené, výstup operácie kombinácia stĺpcov je závislý na vstupných bitoch a pretože lineárna analýza nepracuje s hodnotami nemôže tento vstup žiadnym spôsobom vyjadriť. Z tohto dôvodu, môžeme považovať túto analýzu voči úplnej verzii AES za neuskutočniteľnú. Pretože diferenciálna analýza závisí od pravdepodobnosti nerovnomerného rozdelenia môžeme predpokladať vzhľadom na veľký počet iterácii a väčšiu veľkosť substitučných tabuliek na úrovni iterácie v úplnom variante, že výsledná diferenciálna charakteristika nebude disponovať dostatočne veľkou pravdepodobnosťou zobrazenia k úspešnému útoku.
Záver
Práca prezentuje názornú analýzu odolnosti vybraného redukovaného variantu blokovej šifry so substitučno-permutačnou štruktúrou na úrovni štyroch iterácii, pomocou implementovaného programu voči diferenciálnej a lineárnej kryptoanalýze, ktoré môžeme považovať za minimálnu požiadavku z hľadiska odolnosti komponentov v šifre. Z testovania vyplýva, že implementovaný program predstavuje vhodný nástroj, pre všestrannú analýzu odolnosti existujúcich šifier a znižuje zložitosť výpočtov pri návrhu nových komponentov blokových šifier. Výsledky preukázali potenciál dynamického generovania substitučných tabuliek, ktoré dosahujú porovnateľné výsledky odolnosti ako tabuľky vyjadrené predpisom. Diferenciálna analýza dokázala rekonštruovať kompletný kľúč poslednej iterácie redukovaného tvaru šifry so 4 iteráciami, avšak pre úplný variant môžeme potvrdiť jej odolnosť voči týmto základným útokom. V programe je možné rozšíriť testovanie o variabilnú veľkosť substitučných tabuliek a tým zväčšiť možnosti analýzy odolnosti na komponenty úplných variantov blokových šifier.
Zoznam použitej literatúry
[1]. Cid C., Murphy S., Robshaw M.J.B. Small Scale Variants of the AES. Lecture Notes in Computer Science, 2005, vol. 3557. s. 145-162. Springer, Berlin, Heidelberg. DOI: 10.1007/11502760_10.
[2]. Biham, Eli a Adi SHAMIR. Differential Cryptanalysis of the Data Encryption Standard.New York, NY: Springer New York, 1993. ISBN 978-1-4613-9316-0.
[3]. Matsui, Mitsuru. Linear Cryptanalysis Method for DES Cipher. Advances in Cryptology — EUROCRYPT ’93 . Berlin, Heidelberg: Springer Berlin Heidelberg, 1994, s. 386-397. Lecture Notes in Computer Science. DOI: 10.1007/3-540-48285-7_33.
