Dolovanie znalostí a strojové učenie

V súčastnej informačnej dobe využívame každodenne veľké množstvo informačných technológií, nehovoriac o čase strávenom používaním internetu a mobilných sietí. Všetky naše aktivity za sebou zanechávajú veľké množstvo rozličných dát v podobe informácií o našej polohe, aktivitách, záľubách alebo preferenciách. Všetky tieto dáta predstavujú po ich vhodnom spracovaní potenciál pre získanie rôznych benefitov vrátane ekonomického prospechu. Práve tieto fakty sa stali príčinou, prečo sa na každodenné informácie začalo pozerať ako na ďalší možný využiteľný zdroj. Tento pohľad bol základným kameňom vzniku novej oblasti výskumu dát nazývanej Dolovanie znalostí.

Dolovanie znalostí patrí v súčastnosti k najvýznamnejším a najviac sledovaným oblastiam IT najmä kvôli snahe efektívne využiť každodenné dáta. Jednou z významných disciplín dolovania znalostí je strojové učenie, ktoré predstavuje priamy príklad využitia každodenných informácií – dát pre vytváranie predpovedí o budúcich javoch. V tomto článku bude priblížená problematika strojového učenia s príkladom trénovania modelu za účelom vytvorenia predpovede o budúcich javoch.

Strojové učenie je súbor metód, ktoré umožňujú predpovedanie budúcich javov alebo budúceho správania na základe použitia samoučiacich algoritmov. Schopnosť učenia je nutná hlavne v prípadoch, kedy nie je možné priamo napísať počítačový program na vyriešenie daného problému. Hlavným cieľom strojového učenia je preto vytvorenie samoučiaceho algoritmu, ktorý je schopný učiť sa automaticky bez ľudskej pomoci a zásahov. Strojové učenie rovnako predstavuje jednu z hlavných podoblastí umelej inteligencie, kde je potrebné vytvoriť inteligentný systém, ktorý by bol schopný rôznych inteligentných vlastností vrátane predvídania alebo schopnosti jazyka.

Strojové učenie nachádza uplatnenie hlavne v prípadoch, pri ktorých je potrebné nájsť a extrahovať vnútorné vzťahy a závislosti medzi poskytnutými dátami, pri problémoch ktoré vyžadujú kategorizáciu objektov alebo v oblastiach nasadenia, v ktorých sa predpokladá zmena vplyvov prostredia. Hlavným cieľom strojového učenia je teda vytvorenie efektívnych samoučiacich algoritmov schopných predpovedať budúce výsledky alebo získavať skúsenosti zo získaných dát a pohotovo reagovať na rôzne zmeny v prostredí nasadenia.

Strojové učenia sa delí do troch typov:

• Učenie posilňovaním
• Učenie bez učiteľa
• Učenie s učiteľom

Učenie posilňovaním

Učenie posilňovaním je prístup používaný na pochopenie a automatizáciu cieleného učenia a následného rozhodovania. Toto učenie kladie dôraz na učenie sa jednotlivca z jeho priamej interakcie s prostredím bez možnosti využitia akýchkoľvek vopred určených označených dát. Pri tomto učení nie je študentovi, ktorého predstavuje agent, známe aké kroky je potrebné podniknúť pre nájdenie riešenia ako vo väčšine prístupov strojového učenia. Namiesto toho musí agent zistiť, ktoré akcie prinášajú najväčší prínos, ktorý získa ich skúšaním. V zložitejších prípadoch môžu tieto akcie ovplyvniť nielen okamžité rozhodovanie a odmenu, ale aj nasledujúcu situáciu a všetky ďalšie situácie(odmeny), ktoré nastanú. Práve vykonávanie akcií a oneskorené odmeny predstavujú dve základné charakteristiky učenia posilňovaním.

Učenie bez učiteľa

Učenie bez učiteľa je metodika , ktorá sa zaoberá neoznačenými údajmi, teda údajmi neznámej štruktúry, ktoré sú poskytnuté bez známej výslednej premennej. Na získanie zmysluplných informácií z takýchto dát využíva učenie bez učiteľa metódy klastrovania a redukcie dimenzionality.

Klastrovanie je jednou z najrožšírenejších techník učenia bez učiteľa a umožňuje rozdelenie vstupných dát do skupín-klastrov bez znalosti akýchkoľvek informácií o členstve dát v danej skupine. Tieto klastre predstavujú skupiny dát, ktoré zdieľajú určitú podobnosť a sú viac odlišné od vzoriek v iných klastroch. Najpoužívanejším klastrovacím algoritmom je K-means algoritmus, ktorý rozdeľuje dáta do klastrov pomocou centroidov. Rozdelenie dát prebieha výberom k-centroidov zo vzoriek a priradením vzoriek k najbližšiemu centroidu. Centroid je následne presúvaný do centra vzoriek, ktoré mu boli priradené, pričom sa tento proces opakuje, kým sa neprestane meniť rozloženie klastrov alebo nie je dosiahnutý konečný počet iterácií. Rozdelenie vzoriek je rovnako znázornené na nasledujúcom obrázku :

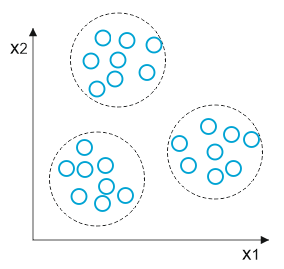
Pri práci s dátami môže dôjsť k výskytu dát vysokých rozmerov. Tieto dáta sú často viacnásobné, nepriame merania zdroja, ktorý nie je možné merať priamo a často tieto dáta predstavujú problém pre spracovanie. Tento problém je možné riešiť pomocou metódy redukcie dimenzionality, ktorá reprezentuje myšlienku učenia algoritmu z nízkorozmernej sady dát vytvorenej z vysoko rozmernej pôvodnej sady. Táto nízkorozmerná sada je vytvorená pomocou komprimácie a zachováva väčšinu relevantných informácií pôvodnej vysokorozmernej sady.

Najčastejšie využívaným algoritmom pre redukciu dimenzionality je PCA algoritmus. Cieľom PCA je identifikovať vzťahy v dátach pomocou korelácie medzi vlastnosťami. Pomocou PCA sa vytvára d*k- dimenzionálna transformačná matica W, ktorá umožňuje mapovanie vzorového vektoru x a následne ho aplikuje na nový k-dimenzionálny priestor vlastností menších rozmerov.

Učenie s učiteľom

Učenie s učiteľom je prístup, pri ktorom sa narozdiel od učenia bez učiteľa algoritmus učí pomocou označených- utriedených dát vytvárať predpovede o neznámych a budúcich dátach. Táto metóda teda predstavuje myšlienku učenia sa pomocou príkladov. Učenie prebieha na základe štúdia označených dátových sád pre následnú identifikáciu nových neoznačených vzoriek. Výsledkom metódy učenia s učiteľom je predikčné pravidlo slúžiace pre klasifikáciu nových neoznačených vzoriek. Medzi základné metódy prístupu učenia s učiteľom patrí regresná analýza a klasifikácia.

Regresná analýza sa využíva na predpoveď kontinuálnych výsledkov a využíva dvojicu vstupných údajov, ktorú predstavuje sada vysvetľujúcich premenných a premenná kontinuálnej odpovede – výsledok. Regresná analýza sa následne snaží nájsť vzájomné vzťahy medzi týmito premennými a vytvoriť tak predpoveď o možných budúcich výsledkoch.

Klasifikácia je metóda, pri ktorej je hlavným cieľom predpoveď správnych označení kategórie nových dát na základe predchádzajúcich pozorovaní. Označenie kategórií možno chápať ako členstvo jednotlivých vzoriek v určitých skupinách. Pre účel klasifikácie slúžia rôzne modely-klasifikátory, pričom každý kasifikátor je špecifický a ich efektivita sa môže líšiť na základe poskytnutých dát. Pre dosiahnutie najlepšej predpovede je preto potrebné zvoliť správny klasifikátor, ktorý je schopný popísať a odlíšiť dátové triedy a koncepty pre účel predpovede kategórií objektov novej sady dát. Typickým príkladom klasifikácie je spam filter, ktorý triedi prijatú poštu na vyžiadanú a spam.

K-najbližší susedia

Jedným z najznámejších algoritmov strojového učenia pre klasifikáciu je algortimus K-najbližších susedov, ktorý sa označuje skratkou KNN. Tento algoritmus si počas procesu učenia zapamätáva celý súbor tréningových dát, z dôvodu ich potreby počas behu. Priebeh algoritmu, ktorý je znázornený na obrázku Obr.2. je možné popísať prostredníctvom 3 krokov :

1. Výber čísla k (ktoré predstavuje počet susedov vzorky) a metriky vzdialenosti.
2. Vyhľadanie k-najbližších susedov vzroky, ktorú chceme klasifikovať.
3. Priradenie označenia vzorky na základe väčšinového hlasu.

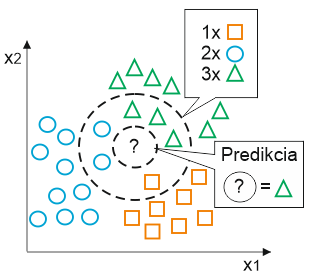
Na základe zvolenej metriky nájde KNN algoritmus k-vzoriek v trénovacej sade dát, ktoré majú najbližšie k neznámej vzorke, ktorú je potrebné klasifikovať. V prípade algoritmu KNN je teda správne zvolenie k počtu susedov a vhodnej metriky vzdialenosti kľúčové pre dosiahnutie čo najlepšieho výsledku.

Vytvorenie modelu metódy učenia s učiteľom

Pre vytvorenie tohto príkladu bolo použité vývojové prostredie Spyder, ktoré poskyuje jednoduchý a efektívny editor pre prácu s programovacím jazykom Python.

Pre prácu boli použité nasledujúce verzie modulov:

• python 2.7.14
• numpy 1.11.1
• scikit-learn 0.17.1

Inštaláciu týchto modulov je možné vykonať po nainštalovaní balíčku Anaconda prostredníctvom Anaconda Prompt, v ktorom je pre zobrazenie a inštaláciu modulov potrebné použiť nasledujúce príkazy:

• conda list – pre zobrazenie verzie modulov
• conda install názov_modulu= (cislo verzie v tvare X.X.X) – pre inštaláciu modulu konkrétnej verzie

Po inštalácií modulov a následnom spustení prostredia Spyder je možné vytvárať vlastný model v už otvorenom súbore untitled0.py, ktorý je možné premenovať.

Prvým krokom vytvárania modelu je načítanie všetkých potrebných modulov, balíčkov a databáz, ktoré budu použité v riešení. V našom prípade ide o modul pyplot, sklearn cross_validation a neighbors, ako aj databázu digits z balíčka datasets, ktorá je jednou zo základných databáz tohto balíčka. Databáza digits, s ktorou budeme pracovať obsahuje rôzne príklady ručne písaných digitálnych číslic, pričom našou úlohou je pomocou modelu predpovede určiť, o akú číslicu ide. Pre implementáciu týchto modulov teda použijeme nasledujúce príkazy:

from sklearn.datasets import load_digits
from sklearn.cross_validation import train_test_split
from sklearn.neighbors import KNeighborsClassifier
import matplotlib.pyplot as plt

Následne je potrebné načítanú databázu uložiť a načítať z nej vzorky a ich označenia. Pre uloženie databázy digits použijeme premennú digits, pričom pre načítanie vzoriek a ich označení použijeme premenné X a y. Tieto kroky vykonáme pomocou nasledujúcich príkazov:

digits= load_digits()
X = digits.data
y = digits.target

Dôležitý krok procesu učenia predstavuje rozdelenie dát na trénovacie a testovacie, ktoré budú slúžiť pre natrénovanie klasifikátora a jeho následné testovanie. Dáta je možné rozdeliť pomocou funkcie train_test_split(), ktorej atribút test_size nastavíme na hodnotu 0.20, ktorá predstavuje percentuálny pomer testovacích dát k trénovacím dátam, čo je v našom prípade 80:20. Do súboru teda pripíšeme nasledujúci riadok kódu :

X_train, X_test, y_train, y_test =train_test_split(X, y,test_size=0.20, random_state=0)

Takto rozdelené dáta je možné spracovať pomocou klasifikátora, ktorý v našom prípade bude reprezentovaný algoritmom k-najbližších susedov. Pri implementácií klasifikátora je potrebné zvoliť vhodný počet susedov a vybrať vhodnú metriku. Tieto atribúty sú v našom prípade nastavené na hodnotu 5 v prípade počtu susedov a pre metriku vzdialenosti bola zvolená metrika ball_tree. Pre implementáciu nášho klasifikátora použijeme nasledujúci príkaz :

clas = KNeighborsClassifier(n_neighbors=3, algorithm='ball_tree')

Samotný proces učenia prebieha pomocou funkcie fit(), ktorá umožňuje trénovanie klasifikátora pomocou trénovacích dát. Po natrénovaní je možné vytvoriť predpoveď o neznámych dátach, ktoré sú v našom prípade reprezentované prostredníctvom tetovacích dát uložených v premennej X_test. Natrénovanie klasifikátora a vytvorenie predpovede vyzerá v kóde nasledovne :

clas.fit(X_train,y_train)
y_predict =clas.predict(X_test)

Úspešnosť predpovede je možné získať pomocou funkcie score(), ktorej argumenty predstavujú testovacie vzorky a ich označenia. Použitie funkcie score môže vyzerať nasledovne :

result = clas.score(X_test, y_test)
print result

Pre znázornenie výsledku použijeme funkciu scatter() modulu pyplot, pomocou ktorej vykreslíme graf závislosti označení trénovacích vzoriek a označení, ktoré vznikli predpoveďou klasifikátora. Pre vytvrorenie grafu teda doplníme nasledujúce riadky :

plt.scatter(y_test, y_predict)
plt.xlabel('True Values')
plt.ylabel('Predictions')

Celý výpis nášho programu by mal vyzerať nasledovne :

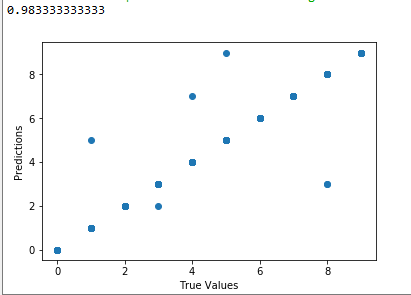
Z výsledného skóre a grafu možno teda povedať, že celý proces trénovania modelu prebehol úspešne a takýto model je možné následne použiť pre vytvorenie predpovedí o nových dátach, ktoré v tomto prípade predstavujú ďalšie neoznačené vzorky ručne písaných číslic.

Predpríprava dát

V mnohých prípadoch sú dáta, ktoré je potrebné analyzovať, často nekompletné, nekonzistentné alebo obahujú šum. Tieto nedostatky môžu byť spôsobené napríklad nedostupnosťou dát, stratou dát z technických príčin alebo ich nezahrnutím z dôvodu domnienky nižšej priority. Práve v takýchto prípadoch sa využívajú rôzne techniky pre predspracovanie dát, ktorých hlavným cieľom je zabezpečenie lepšej kompletnosti a kvality dát. Medzi známe techniky predspracovania dát patria :

• Imputácia
• Mapovanie kategorických dát
• Normalizácia a štandardizácia

Imputácia je nástroj predspracovania dát, ktorý umožňuje doplnenie chýbajúcich alebo poškodených dát. Doplnenie týchto dát je možné pomocou trojice stratégií. Stratégia mean umožňuje nahradenie chýbajúcich hodnôt priemernými hodnotami stĺpca, v ktorom sa nachádza chýbajúca hodnota. Pri stratégií median dochádza k nahradeniu chýbajúcej hodnoty median hodnotou daného stĺpca. Poslednou stratégiou je stratégia most_frequent, ktorá umožňuje nahradenie hodnoty najčastejšie sa vyskytujúcou hodnotou v danom stĺpci.

Kategorické dáta často predstavujú problém pre učiace sa algoritmy. Tento problém je možné riešiť pomocou mapovania, ktoré umožňuje vytvorenie mapy, na základe ktorej je možné konvertovať reťazce na číselné hodnoty. Príkladom použitia mapy môže byť napríklad označenie veľkosti oblečenia, ktoré je možné znázorniť v nasledovnom usporiadaní S < M < L < XL. Mapovanie takýchto dát môže vyzerať nasledovne: S : 0 , M : 1, L : 2, XL : 3. Takéto mapovanie odzrkadľuje aj reálne podmienky, kde platí 0 < 1 a S < M.

V prípade, že sú dáta zaznamenané v rozličných rozsahoch môže pri trénovaní nastať problém, pri ktorom je výsledok ovplyvnený vlastnosťami, ktoré sú mimo rozsah veľkostí ostatných vlastností z dátovej sady. Pre zmenu týchto rozsahov sa používa technika normalizácie a štandardizácie. Normalizácia predstavuje zmenu rozsahu dát na rozsah intervalu [0,1], pri štandardizácií sa stĺpce vlastností zoradia na nulový priemer, čo zachová stĺpce vo forme bežného rozdelenia.

Trénovanie modelu s predprípravou dát

V predchádzajúcom prípade sme si ukázali, ako vyzerá vytvorenie a trénovanie modelu strojového učenia s učiteľom. Jedným z prvých krokov príkladu bolo načítanie databázy digits, ktorá predstavuje cvičnú databázu z balíčka datasets. Tieto databázy predstavujú úplné sady dát, bez akýchkoľvek nedostatkov. V reálnych podmienkach však môže dôjsť k získaniu rôznych poškodených a nekompletných dát, ktoré je potrebné spracovať pred samotným trénovaním modelu. Spracovanie takýchto dát si priblížime v nasledujúcom príklade.

Pre tento účel využijeme databázu iris z balíčka predefinovaných databáz datasets, ktorá obsahuje rozmery okvetných lístkov jednotlivých rastlín, na základe ktorých je možné určiť o aký druh rastliny ide. Táto databáza bola mierne upravená pre zabezpečenie výskytu neznámych a kategorických hodnôt.

Pre načítanie databázy využijeme nástroj pickle balíčka pandas, ktorý umožňuje ukladanie a načítavanie dátových sád. Pre načítanie označení daných dát zo sady využijeme funkciu load() balíčka numpy, ktorý je rovnako potrebné importovať. Riešenie bude teda obsahovať nasledujúce riadky kódu :

import numpy as np
import pandas as pd

dset=pd.read_pickle('X_dset')
y_dset=np.load('y_dset.npy')

Následným spustením nášho programu a kliknutím na položku variable explorer v pravom hornom okne prostredia Spyder, sa nám zobrazia všetky použité premenné nášho riešenia. Kliknutím na premennú dset, ktorá predstavuje našu databázu, je možné ju zobraziť :

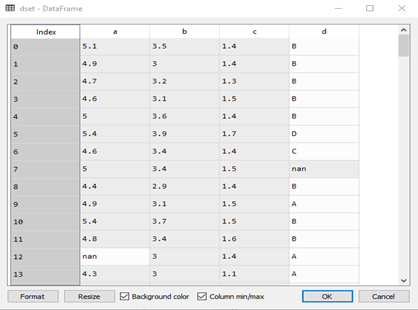
Pri pohľade na databázu je vidieť že táto databáza obsahuje chýbajúce hodnoty, ktoré sú nahradené označením nan – not a number, ako aj reťazce vyžadujúce aplikáciu mapovania. Ďalším krokom riešenia, ktoré predstavuje samotnú predprípravu dát je teda vytvorenie mapovania a jeho následná aplikácia na našu databázu. Tieto kroky je možné vykonať pomocou nasledujúcich príkazov :

d_mapping = {0.1:'A',0.2:'B',0.3:'C',0.4:'D',0.5:'V',0.6:'E',1:'F',1.1:'G',1.2:'H',
             1.3:'CH',1.4:'I',1.5:'J',1.6:'K',1.7:'L',1.8:'M',1.9:'N',2:'O',2.1:'P',
             2.2:'R',2.3:'S',2.4:'T',2.5:'U'}

inv_d_mapping = {v: k for k, v in d_mapping.items()}
dset['d'] = dset['d'].map(inv_d_mapping)

Touto aplikáciou mapovania na našu databázu sme dosiahli nahradenia reťazcov hodnotami, ktoré sme použili v mapovaní. Naša databáza by preto mala vyzerať nasledovne :

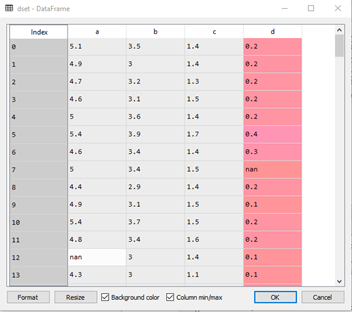
V databáze sa však naďalej vyskytujú chýbajúce hodnoty. Pre ich riešenie je potrebné importovať a aplikovať nástroj imputácie, ktorý umožňuje nahradenie chýbajúcich hodnôt. Hodnoty budeme nahrádzať pomocou stratégie median, ktorá chýbajúce hodnoty nahradí median hodnotou daného stĺpca, v ktorom sa chýbajúca hodnota nachádza. Nástroj imputácie je možné aplikovať pomocou nasledujúcich príkazov :

from sklearn.preprocessing import Imputer
imp= Imputer(missing_values='NaN', strategy='median', axis=0)
dset=imp.fit_transform(dset)

Po aplikácií nástroja imputácie by mala databáza vyzerať nasledovne:

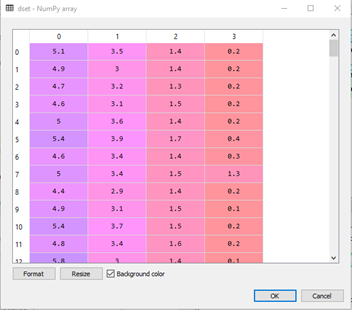
Takto upravené dáta je možné použiť pre trénovanie ľubovoľného klasifikátora, pričom v našom prípade využijeme klasifikátor náhodných lesov. Do nášho riešenia, teda vložíme nasledujúce riadky :

from sklearn.ensemble import RandomForestClassifier
forrest=RandomForestClassifier(max_depth=5, random_state=0)
clas=forrest
clas.fit(X_train,y_train)
y_predict =clas.predict(X_test)

Pre výpis úspešnosti predpovede použijeme funkciu accuracy_score() z balíčka metrics, ktorý je rovnako potrebné importovať. Dopíšeme teda nasledujúce príkazy :

from sklearn.metrics import accuracy_score
v=accuracy_score(y_predict,y_test)
print v

Keďže výsledná hodnota predpovede dosahuje úspešnosť 0.966, čo je vlastne 96,6 percentná úspešnosť predpovede, môžeme toto trénovanie modelu považovať za úspešné a takto natrénovaný model je teda možné použiť pre identifikáciu rastlín na základe nových rozmerov okvetných lístkov, pri ktorých je neznáme akej rastline patria.

Záver

Strojové učenie predstavuje v súčastnosti pomerne mladú a atraktívnu vednú disciplínu, ktorá nám umožňuje efektívne využívať rôznorodé dáta pre získanie užitočných poznatkov, ktoré je možné následne uplatniť pre predpovedanie budúcich javov. V tomto článku bol predstavený stručný úvod do tejto problematiky s názornými ukážkami problémov, ktoré by mali pomôcť čitateľovi pochopiť základné princípy strojového učenia a následne ho tak pripraviť pre ďalšie prípadné štúdium tejto problematiky.